Ma and Pa of the USA: Massachusetts and Pennsylvania

Years ago I observed the aptness of the US postal abbreviations (introduced in 1963) of MA for Massachusetts and PA for Pennsylvania, as these states are indeed the Ma (mother) and Pa (father) of the USA, playing preeminent roles among the Thirteen Colonies during the American Revolution.

I supposed then that others must have thought of this before me. However as Google did not turn up any evidence of others making this observation, I hereby share it.

A conspectus of the crucial roles of Massachusetts and Pennsylvania in the American Revolution follows:

Revolutionary Massachusetts (source: Wikipedia)

Massachusetts was a center of the movement for independence from Great Britain, earning it the nickname, the "Cradle of Liberty". Colonists here had long had uneasy relations with the British monarchy, including open rebellion under the Dominion of New England in the 1680s. The Boston Tea Party is an example of the protest spirit in the early 1770s, while the Boston Massacre escalated the conflict. Anti-British activity by men like Sam Adams and John Hancock, followed by reprisals by the British government, were a primary reason for the unity of the Thirteen Colonies and the outbreak of the American Revolution. The Battles of Lexington and Concord initiated the American Revolutionary War and were fought in the Massachusetts towns of Concord and Lexington. Future President George Washington took over what would become the Continental Army after the battle.
His first victory was the Siege of Boston in the winter of 1775–6, after which the British were forced to evacuate the city. The event is still celebrated in Suffolk County as Evacuation Day. In 1777, George Washington and Henry Knox founded the Arsenal at Springfield, which catalyzed many innovations in Massachusetts' Connecticut River Valley.

Boston

Boston was the center of revolutionary activity in the decade before 1775, with Massachusetts natives Samuel Adams, John Adams, and John Hancock as leaders who would become important in the revolution. Boston had been under military occupation since 1768. When customs officials were attacked by mobs, two regiments of British regulars arrived. They had been housed in the city with increasing public outrage.

In Boston on March 5, 1770, what began as a rock-throwing incident against a few British soldiers ended in the shooting of five men by British soldiers in what became known as the Boston Massacre. The incident caused further anger against British authority in the commonwealth over taxes and the presence of the British soldiers.

Boston Tea Party

One of the many taxes protested by the colonists was a tax on tea, imposed when Parliament passed the Townshend Acts, and retained when most of the provisions of those acts were repealed. With the passage of the Tea Act in 1773, tea sold by the British East India Company would become less expensive than smuggled tea, and there would be reduced profit making opportunities for Massachusetts merchants engaged in the tea trade. This led to protests against the delivery of the company's tea to Boston. On December 16, 1773, when a tea ship of the East India Company was planning to land taxed tea in Boston, a group of local men known as the Sons of Liberty sneaked onto the boat the night before it was to be unloaded and dumped all the tea into the harbor, an act known as the Boston Tea Party.

The Boston Tea Party prompted the British government to pass the Intolerable Acts in 1774 that brought stiff punishment on Massachusetts. They closed the port of Boston, the economic lifeblood of the Commonwealth, and reduced self-government. The Patriots formed the Massachusetts Provincial Congress after the provincial legislature was disbanded by Governor Gage. The suffering of Boston and the tyranny of its rule caused great sympathy and stirred resentment throughout the Thirteen Colonies. On February 9, 1775, the British Parliament declared Massachusetts to be in rebellion, and sent additional troops to restore order to the colony. With the local population largely opposing British authority, troops moved from Boston on April 18, 1775, to destroy the military supplies of local resisters in Concord. Paul Revere made his famous ride to warn the locals in response to this march. On the 19th, in the Battles of Lexington and Concord, where the famous "shot heard 'round the world" was fired, British troops, after running over the Lexington militia, were forced back into the city by local resistors. The city was quickly brought under siege. Fighting broke out again in June when the British took the Charlestown Peninsula in the Battle of Bunker Hill after the colonial militia fortified Breed's Hill. The British won the battle, but at a very large cost, and were unable to break the siege. Soon afterwards General George Washington took charge of the rebel army, and when he acquired heavy cannon in March 1776, the British were forced to leave, marking the first great colonial victory of the war. This was the last significant fighting in present-day Massachusetts; the 1779 Penobscot Expedition took place in the District of Maine, then part of the Commonwealth. In May 1778, the section of Freetown that later became Fall River was raided by the British, and in September 1778, the communities of Martha's Vineyard and New Bedford were also subjected to a British raid.

The fighting brought to a head the political opposition to the crown that had been brewing throughout the colonies, and on July 4, 1776, the United States Declaration of Independence was adopted in Philadelphia. It was signed first by Massachusetts resident John Hancock, president of the Continental Congress. Soon afterward the Declaration of Independence was read to the people of Boston from the balcony of the State House.

*************************************************

Revolutionary Pennsylvania (source1, source2)



First and Second Continental Congresses


The economic importance and central location of Philadelphia, Pennsylvania in the Thirteen Colonies made it a natural center for America's revolutionaries. When the Founding Fathers of the United States convened the First Continental Congress in Philadelphia in 1774, 12 colonies sent representatives.


The Second Continental Congress, which also met in Philadelphia (in May, 1775), drew up and signed the Declaration of Independence in Philadelphia but when that city was captured by the British, the Continental Congress escaped westward, meeting at the Lancaster courthouse on Saturday, September 27, 1777, and then to York. There they drew up the Articles of Confederation that formed 13 independent colonies into a new nation.



Constitutional Convention

The Constitutional Convention took place from May 14 to September 17, 1787, in Philadelphia, Pennsylvania, to address problems in governing the United States of America, which had been operating under the Articles of Confederation following independence from Great Britain. Although the Convention was intended to revise the Articles of Confederation, the intention from the outset of many of its proponents, chief among them James Madison and Alexander Hamilton, was to create a new government rather than fix the existing one. The delegates elected George Washington to preside over the convention. The result of the Convention was the United States Constitution, placing the Convention among the most significant events in the history of the United States.

Pennsylvania became the second state to ratify the U.S. Constitution on December 12, 1787, five days after Delaware became the first.


Temporary US Capital  (source)


Philadelphia served as the temporary capital of the United States, 1790–1800, while the Federal City was under construction in the District of Columbia.

The simple geometry of sun, moon, and star paths

How to determine the sun, moon, and stars' path across the sky at any latitude, and at any time of the year.



A challenging geometric problem: Derive the sun path (or day arc of the sun), the sun's trajectory in the sky, given a latitude, and the day of the year, e.g. 35° N, April 23.

I tried, and failed at first, to deduce accurately the shape of the sun paths. I then found sun path diagrams for specific latitudes here (for selected locations) and here* (for selected latitudes). See examples at the end of this post.


*carrying a wrong statement: "For a site located in the tropics between 23.5°N and 23.5°S, the sun will be in the North during the summer and in the South during the Winter." The correct statement is: "For a site located in the tropics between 23.5°N and 23.5°S, the sun will occupy only azimuths north of the E-W line (in the North) at the summer solstice and occupy only azimuths south of the E-W line (in the South) at the Winter solstice."


However, these sun path diagrams (linked above) do not reveal the simple geometry of the sun paths. Having fully thought through and understood the sun path geometry (I've not yet found a full description of this geometry online), I'll now briefly describe it:

Sun path geometry

These three diagrams show how sun paths can be readily determined.

Note that in the 50° N (latitude) diagram, the angle 40° (of the noon sun at the equinoxes) is computed thus: 40°=90°-50°. In general, the angle of the noon sun (from the horizon) at the equinoxes equals (90° - latitude). Also note that the angle between the noon sun at the equinox and the noon sun at the (summer and winter) solstice is always 23.5°, whatever the latitude. You can therefore draw a similar diagram for any latitude. (For example, the sun paths at 40°N are as follows.)

sun paths at 40°N

Precisely stated, the sun paths at latitude L°N are formed by rotating the north polar (90°N) sun paths (shown above) by (90-L)°, clockwise when viewing from E to W, about the E-W axis.

The sun paths at latitude L°S are formed by rotating the north polar (90°N) sun paths by (90+L)°, clockwise when viewing from E to W, about the E-W axis.


More concisely (but using technical terms), when the sun's declination is d° (at a certain time of the year), the sun path is the d° small circle (parallel) of the celestial sphere. The latitude of the observer on earth determines the small circle's position in the sky (i.e. the degree of rotation from the north polar sun path).


Why do the sun paths follow the simple geometry shown above?

Standing upright at θ° N

It is easy to see that, when you stand upright at the north pole, the sun paths are as shown in the 90° N diagram. 

Standing upright at any other latitude (as shown in the above diagram) causes the sun paths to rotate in the way described earlier.


Sun's declination

To find out the sun's declination for any day of the year (+23.5° for the June solstice, 0° for the equinoxes, and -23.5° for the December solstice), you can use this table.



*******************************************************************************

Star Paths


The reason for the sun paths' geometry in fact also applies to the trajectory across the sky of all relatively stationary celestial bodies, i.e. stars and the moon.

Note that when the sun's declination is +23.5° (for the June solstice), the sun path is the +23.5° (23.5°N) small circle (parallel) of the celestial sphere. In general, when the sun's declination is d° (at a certain time of the year), the sun path is the d° small circle of the celestial sphere. The latitude of the observer on earth determines the small circle's position in the sky (i.e. the degree of rotation from the north polar sun path).

This fact is also true of all stars. If a star's declination is d°, then its path across the sky is the d° small circle of the celestial sphere. The latitude of the observer on earth determines the small circle's position in the sky (i.e. the degree of rotation from the north polar star path).

The North Star (northern pole star)'s declination is +90°, and therefore appears stationary in the sky. All other stars appear to rotate around the northern and (imaginary) southern pole stars (currently there is no star at declination -90°).

Long exposure (45 min) photo (facing north) of the northern sky (50°N) 

around North Star, showing  the +40° to +90° small circles

(which are completely visible in the sky) of the celestial sphere (source)

Moon Path

Because the moon's orbital plane around the earth is close to the earth's orbital plane around the sun (the ecliptic), the moon's declination ranges from -23.5° to +23.5° (approximately; for a precise range, see here) through a lunar cycle (a sidereal month of  27.32 days, slightly shorter than the period of moon's phases (synodic month) of 29 days, 12 hours, 44 minutes) (see diagrams below).

Moon's declination, June 2012 (source)

Moon's declination, July 2012

Therefore the moon path is approximately within the range of the sun path, from -23.5° to +23.5° parallel.

For detailed data on lunar declination from 2001-2100, see here.

Lunar Phases and Appearance (Shape) of the Moon 

Appearance of the Moon at the North Pole. The upper part of the diagram is not to scale,

 as the Moon is much farther from the Earth than shown here.(source)

 

At any phase of the moon, the lit portion of the moon indicates the sun's position relative to the moon. The moon moves along a d° small circle of the celestial sphere, where d° is the moon's declination.

At the north pole, the moon's appearance is as shown above, and right (→) is the direction of the moon's advance along the small circle of the celestial sphere. The first quarter moon has the right half lit. The last quarter moon has the left half lit. The moon moves right along a celestial small circle.

Identically with the sun path and star paths, the moon's path (a celestial small circle) occupies a rotated position (from its north polar position) in the sky according to latitude. The first quarter moon's lit half always points to the moon's direction of advance through the night. Likewise the last quarter moon's dark half always points to the moon's direction of advance through the night. (see photos below, possibly taken from space)

At the equator, the first quarter moon rises with top half lit, and sets with the bottom half lit. The last quarter moon rises with the bottom half lit, and sets with the top half lit.

At the south pole the The first quarter moon has the left half lit. The last quarter moon has the right half lit. The moon moves left.

First quarter moon rising (noon, invisible),

or last quarter moon setting (noon, invisible), at the equator

First quarter moon setting (midnight),

or last quarter moon rising (midnight), at the equator

First quarter moon rising (around noon, invisible) at mid Northern hemisphere, or 

last quarter moon setting (around noon, invisible) at mid Southern hemisphere.

First quarter moon setting (around midnight) at mid Northern hemisphere, or 

last quarter moon rising (around midnight) at mid Southern hemisphere.

Last quarter moon rising (around midnight) at mid Northern hemisphere, or 

first quarter moon setting (around midnight) at mid Southern hemisphere.

Last quarter moon setting (around noon, invisible) at mid Northern hemisphere, or 

first quarter moon rising (around noon, invisible) at mid Southern hemisphere.

2012 Phases of the Moon Universal Time New Moon First Quarter Full Moon Last Quarter d h m d h m d h m d h m Jan 1 6 15 Jan 9 7 30 Jan 16 9 08 Jan 23 7 39 Jan 31 4 10 Feb 7 21 54 Feb 14 17 04 Feb 21 22 35 Mar 1 1 21 Mar 8 9 39 Mar 15 1 25 Mar 22 14 37 Mar 30 19 41 Apr 6 19 19 Apr 13 10 50 Apr 21 7 18 Apr 29 9 57 May 6 3 35 May 12 21 47 May 20 23 47 May 28 20 16 Jun 4 11 12 Jun 11 10 41 Jun 19 15 02 Jun 27 3 30 Jul 3 18 52 Jul 11 1 48 Jul 19 4 24 Jul 26 8 56 Aug 2 3 27 Aug 9 18 55 Aug 17 15 54 Aug 24 13 54 Aug 31 13 58 Sep 8 13 15 Sep 16 2 11 Sep 22 19 41 Sep 30 3 19 Oct 8 7 33 Oct 15 12 02 Oct 22 3 32 Oct 29 19 49 Nov 7 0 36 Nov 13 22 08 Nov 20 14 31 Nov 28 14 46 Dec 6 15 31 Dec 13 8 42 Dec 20 5 19 Dec 28 10 21

(source)

Rising and setting of the Moon

The sun is at its upper culmination (highest point in the sky), crossing the observer's meridian, at noon. The new moon is at its upper culmination also at noon (i.e. the moon is then between the sun and the earth). The moon culminates (at its highest point in the sky) at 3 pm at waxing crescent, 6 pm at first quarter, 12 midnight at full moon, and 6 am at last quarter. (see Lunar phase)

At the equator, the moon rises about 6 hours before culmination, and sets about 6 hours after culmination. Elsewhere, the declination of the moon and the observer's latitude determines the exact time of the moon's rising and setting..

Thus, in the following table, the lunar phase determines the moon's meridian passing (upper culmination) time. The moon's declination and latitude  determine the moonrise and moonset azimuth and the meridian passing altitude. The lunar phase, the moon's declination, and latitude determine the moonrise and moonset time.

For similar information on the moon path (and the sun path) at various locations, see here.

Rising and setting times for the Moon. London, July 2012  (source)

All times are in local time for London (BST=UTC+1h)
(table explanation) (: southeast, : east,  : southwest)

	Time,local		Azimuth		Meridian Passing
Date	Moonrise	Moonset	Moonrise	Moonset	Time	Altitude	Distance	Illuminated	Phase
							(km)
1 Jul 2012	- 19:04	02:27 -	- 126°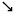	235° -	23:14	15.9°	362,389	95.1%
2 Jul 2012	- 20:05	03:23 -	- 126°	233° -
3 Jul 2012	- 20:54	04:30 -	- 123°	235° -	00:16	16.4°	363,485	99.0%	Full Moon at 19:52
4 Jul 2012	- 21:32	05:45 -	- 117°	239° -	01:16	18.4°	366,204	99.8%
5 Jul 2012	- 22:02	07:04 -	- 111°	245° -	02:14	21.7°	370,353	97.7%
6 Jul 2012	- 22:27	08:22 -	- 103°	252° -	03:07	25.9°	375,566	92.9%
7 Jul 2012	- 22:49	09:37 -	- 95°	260° -	03:56	30.6°	381,369	86.1%
8 Jul 2012	- 23:09	10:49 -	- 88°	269° -	04:43	35.5°	387,254	77.7%
9 Jul 2012	- 23:29	11:59 -	- 80°	276° -	05:28	40.4°	392,751	68.3%
10 Jul 2012	- 23:50	13:07 -	- 73°	284° -	06:12	45.0°	397,473	58.5%
11 Jul 2012		14:13		291°	06:55	49.2°	401,138	48.5%	Third Quarter at 02:48
12 Jul 2012	00:13	15:18	67°	296°	07:40	52.8°	403,571	38.7%
13 Jul 2012	00:39	16:21	62°	301°	08:25	55.7°	404,701	29.5%
14 Jul 2012	01:11	17:21	57°	305°	09:12	57.8°	404,561	21.0%
15 Jul 2012	01:49	18:16	55°	306°	10:00	59.0°	403,277	13.6%
16 Jul 2012	02:34	19:04	54°	306°	10:50	59.2°	401,050	7.5%
17 Jul 2012	03:28	19:45	55°	303°	11:40	58.3°	398,128	3.1%
18 Jul 2012	04:29	20:20	58°	299°	12:30	56.3°	394,760	0.6%
19 Jul 2012	05:36	20:50	63°	294°	13:19	53.3°	391,174	0.3%	New Moon at 05:25
20 Jul 2012	06:46	21:15	69°	287°	14:08	49.5°	387,548	2.2%
21 Jul 2012	07:59	21:38	76°	280°	14:55	44.9°	384,013	6.4%
22 Jul 2012	09:12	22:00	84°	272°	15:43	40.0°	380,654	12.9%
23 Jul 2012	10:27	22:22	92°	264°	16:31	34.9°	377,523	21.3%
24 Jul 2012	11:44	22:45	101°	256°	17:20	29.8°	374,659	31.4%
25 Jul 2012	13:01	23:12	109°	248°	18:11	25.1°	372,108	42.7%
26 Jul 2012	14:19	23:43	116°	241°	19:05	21.0°	369,955	54.5%	First Quarter at 09:56
27 Jul 2012	15:36	-	122°	-	20:02	18.0°	368,335	66.2%
28 Jul 2012	- 16:49	00:23 -	- 126°	237° -	21:01	16.3°	367,431	77.1%
29 Jul 2012	- 17:52	01:12 -	- 126°	234° -	22:02	16.1°	367,439	86.4%
30 Jul 2012	- 18:45	02:13 -	- 125°	234° -	23:02	17.4°	368,522	93.5%
31 Jul 2012	- 19:27	03:23 -	- 120°	237° -	23:59	20.0°	370,752	98.1%

******************************************************

Some sun path diagrams


Equator



London, UK (51.4°N)



Arctic circle

Source: All the following diagrams are from here, where you can specify the location and date of the sun path you want.

Sun path at Qanaq (Qaanaaq), Greenland (77°29′00″N, above the Arctic Circle) at summer solstice

Sun path at Trondheim (63°25′N, just below the Arctic Circle) at summer solstice

Sun path at Hong Kong (22°19′N, near Tropic of Cancer) at summer solstice



Sun path at Quito (near the Equator, 0°13′S) at March equinox

Sun path at Quito (near the Equator, 0°13′S) at June solstice

Sun path at Bangkok, Thailand (13°55′N) at June solstice

Sun path at Bangkok, Thailand (13°55′N) at December solstice

Why does the setting waxing crescent moon appear more horizontal (seem to smile more) in winter than in summer in the Northern hemisphere?

A reader of this post has asked about the phenomenon that the waxing crescent moon (following the new moon), when observed setting in the west in mid-northern latitudes, appears to be more horizontal (like a smile) in winter than in summer.

A common, but wrong, interpretation is that the moon path in winter is different from that in summer, as shown in this diagram:

Wrong picture! 

There is absolutely no reason why the moon path should differ in this manner.

The moon path intercepts the western  horizon at exactly the same angle (given any fixed latitude) at all times of the year. 

The following is the right picture, showing that the crescent moon tilts but the moon path remains the same:

The explanation of this tilt is as follows:

For background knowledge, first read the section above on Lunar Phases and Appearance (Shape) of the Moon.

Appearance of the Moon at the North Pole

For the Moon to appear (called the standard appearance) as shown in the above diagram, a specific relation (called the special configuration) on the positions of the earth, the moon and the sun must hold.

You may skip the following description of the special configuration, the understanding of which requires some careful thought.

*****************************************

Special Configuration

Consider an observer K of the Moon on Earth's North Pole. The boundary C of the Moon's observable hemisphere (assuming full moon) is a great circle. Let's impose circles of longitude (meridians) on the moon thus: Let the top and bottom of the Moon (on C) as seen by K be the Moon's poles. A Moon's meridian is a great circle, such as C, that contains both poles.

For the Moon to appear as shown above with the standard appearance, the boundary of the Moon's Sun-illuminated hemisphere must be a meridian.

This in turn implies that the Sun must lie on the Moon's Equatorial plane (the plane normal to its polar axis and containing its center). This is the special configuration mentioned above.

*******************************************

Near the June solstice, the sun's declination is high (near +23.5°). Thus it is probable the the sun's declination is higher than what the special configuration requires, which in turn causes the moon shape as seen in the North Pole to tilt in the following manner compared with the standard appearance because the sun now illuminates a different portion of the moon.

Shape of first quarter moon (tilt exaggerated) at North Pole  

Near the December solstice, the sun's declination is low (near -23.5°). Thus it is probable the the sun's declination is lower than what the special configuration requires, which in turn causes the moon shape as seen in the North Pole to tilt in the following manner compared with the standard appearance because the sun now illuminates a different portion of the moon.

Shape of first quarter moon (tilt exaggerated) at North Pole

The moon shape seen at any latitude likewise tilts (see the section above on Lunar Phases and Appearance (Shape) of the Moon for how latitude determines moon shape).

This explains why the waxing crescent moon, when setting in the northern hemisphere, probably smiles more in winter than in summer.

***************************************

The following table gives the approximate data on the Moon's declination, the Sun's declination as required by the special configuration (A), the Sun's actual declination (B), and their difference (B-A), two days after the new moons (i.e. at the first observable waxing crescent moon) in 2015. 

The sun's deviation from its special configuration is 11.49° on 7/18/2015, and -13.94° on 2/21/2015, making a total deviation of 25.43°.  This is certainly noticeable, and explains the above mentioned shift in moon shape.

Date	moon's declination	A. special config	B. sun's declination	B-A
1/22/2015	-8.40	-7.65	-19.87	-12.22
2/21/2015	3.37	3.07	-10.87	-13.94
3/22/2015	9.98	9.08	0.40	-8.68
4/21/2015	17.15	15.58	11.65	-3.93
5/20/2015	18.38	16.69	19.85	3.16
6/18/2015	17.08	15.51	23.40	7.89
7/18/2015	10.60	9.64	21.13	11.49
8/16/2015	4.83	4.40	13.93	9.53
9/15/2015	-5.13	-4.67	3.27	7.94
10/15/2015	-13.73	-12.48	-8.30	4.18
11/14/2015	-18.20	-16.53	-18.07	-1.54
12/13/2015	-17.77	-16.14	-23.12	-6.98

The sun's pattern of deviation from its special configuration varies from year to year. The maximum declination of the moon plays an important role in the pattern.

October 2015 sees a minor lunar standstill, when the moon's maximum declination is at its minimum.

The following tabulates the same set of data for 2006. In June 2006 there was a major lunar standstill, when the moon's maximum declination is at its maximum.

Date	moon's declination	A. special config	B. sun's declination	B-A
1/2/2006	-24.23	-21.95	-22.85	-0.90
1/31/2006	-18.12	-16.45	-17.63	-1.18
3/2/2006	-6.33	-5.76	-7.87	-2.11
3/31/2006	7.57	6.89	3.62	-3.27
4/30/2006	20.50	18.60	14.20	-4.40
5/29/2006	28.49	25.75	21.50	-4.25
6/28/2006	24.52	22.21	23.12	0.91
7/27/2006	19.90	18.06	19.45	1.39
8/26/2006	9.53	8.67	11.07	2.40
9/24/2006	-3.85	-3.51	0.03	3.54
10/24/2006	-17.50	-15.89	-11.22	4.67
11/23/2006	-28.44	-25.70	-20.03	5.67
12/22/2006	-24.52	-22.21	-23.50	-1.29

The largest positive deviation of the sun's declination (5.67°) in 2006 occurred near the December solstice, and the largest negative deviation of the sun's declination (-4.40°) in 2006 occurred near the June solstice. The magnitude of the deviations were small throughout the year. 

The above mentioned shift in crescent moon shape is therefore not an unchanging phenomenon observable every year.


* For computing column A. above, I used the geometry and trigonometry here.

   *******************************************************************